MV's blog

Left Leaning Red-Black Trees

A leaft leaning red-black tree is a way to implement a 2-3 tree. The idea behind red-black trees is to encode 2-3 trees by starting with standard BST (which are made up of 2-nodes) and adding an extra information to encode 3-nodes. That extra information is the color of the link between two nodes. Specifically, we represent 3-nodes as two 2-nodes connected by a single red link that leans left (one of the two nodes is the left child of the other), and we think of the black links as the links that bind the 2-3 tree together.

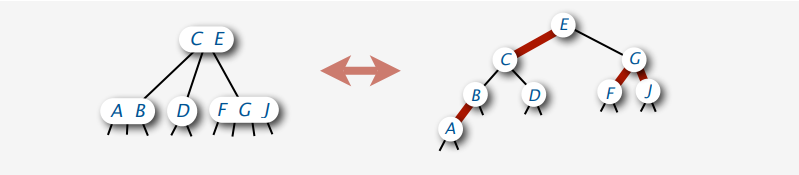
LLRBT must satisfy the following invariants:

• The leaf nodes must have equal black height (same number of black links to the root)
• There cannot be two consequitive red links
• Red links lean left

Search

Searching is the same as searcing in a regular BST. Start from the root and compare the key's values, if the key to be found is less than the root's key, go left, if it is greater go right, repeat until a key with the same value is found in which return the value asssociated with that key, or if no key is found return null;

Insert

When inserting, the first step is pretty much the same as in a standard BST - find the appropriate place and insert the node. The only difference is that in a RBT we are always inserting a node with a red link. After that is done, the tree can be in one of 3 states.

The first one is when the insert was done in a left link(node) of black node. In which case the tree satisfies all of the invariants and the insert is done.

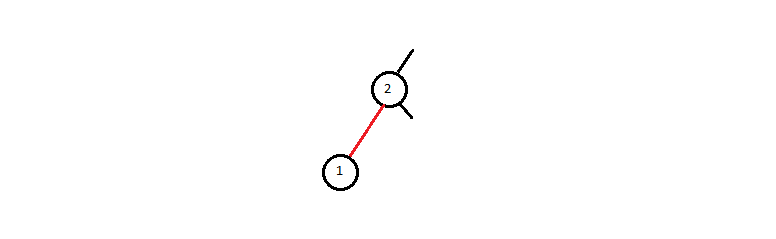
The second one is when the insert was done in a right link(node) of a black node. In which case the left leaing invariant is broken and needs to be fixed. The invariant is fixed by rotating the higher node left.

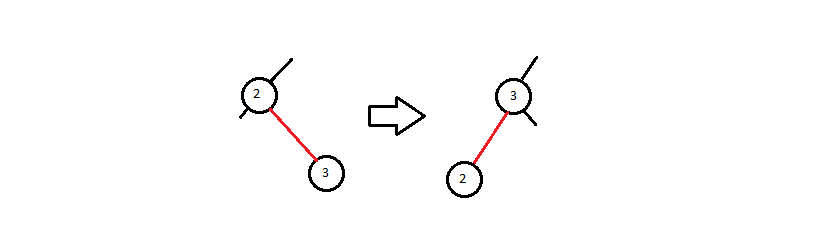
function rotateLeft(
  node: RBTNode<Key, Value>,
): RBTNode<Key, Value> {
  // cast is safe, it cannot be null because it is checked in balance()
  const x: RBTNode<Key, Value> = node.right as RBTNode<
    Key,
    Value
  >;
  const nodeRight: RBTNode<Key, Value> | null = x.left;
  x.left = node;
  x.color = node.color;
  node.right = nodeRight;
  node.color = 'RED';

  return x;
}

And the third one is if the insert was done in a left link(node) of red node. In which case the invariant that there cannot be two consequitive red links is broken and needs to be fixed. The invariant is fixed by rotating the first red node right and swaping colors.

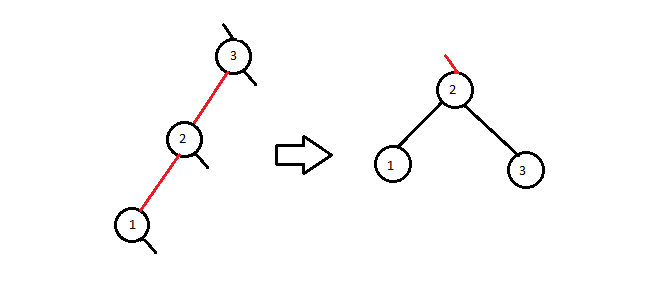
function rotateRight(
  node: RBTNode<Key, Value>,
): RBTNode<Key, Value> {
  // cast is safe, it cannot be null because it is checked in balance()
  const x: RBTNode<Key, Value> = node.left as RBTNode<
    Key,
    Value
  >;
  const nodeLeft: RBTNode<Key, Value> | null = x.right;
  x.right = node;
  x.color = node.color;
  node.left = nodeLeft;
  node.color = 'RED';

  return x;
}

function flipColors(node: RBTNode<Key, Value>): void {
  node.flipColor();
  node.left?.flipColor();
  node.right?.flipColor();
}

There can also be a fourth one where the insert was done in a red link of a red node but that is covered by first rotating the node right in which case a double red would appear and be fixed by the third case.

Inserting: 7 2 3 4 8 covers all cases

Delete

Just as we are always inserting a red node, we always want to remove a red node. If we don't do that, there are 6 different cases that can occur to be rebalanced after the delete operation. However there is a more elegant solution, where on the way down while searching for the node we make all the encountered nodes either 3 nodes or 4 nodes. Then once we delete the node in either a 3 node or a 4 node, on the way up we fix the nodes - breakup the 4 nodes into 2 two nodes.

To understand the delete operation its useful to first take a look at the delete max and delete min operations.

Delete Max

To delete the max element, we search the right spine of the tree, and as stated above we want the search to end in either a 3-node or a 4-node; removing a 2 node would destroy the balance. So on the way down the search path we transform the tree by either rotating the red links to the right or borrowing from a sibling.

function delMax(
  node: RBTNode<Key, Value> | null,
): RBTNode<Key, Value> | null {
  if (node == null) return null;

  // Lean 3-nodes to the right
  if (RBTNode.isRed(node.left)) node = this.rotateRight(node);

  if (node.right === null) return null;

  // Borrow from sibling if necessary
  if (
    !RBTNode.isRed(node.right) &&
    !RBTNode.isRed(node.right.left)
  )
    node = this.moveRedRight(node);

  node.right = this.delMax(node.right);

  // Fix right leaning red links and eliminate 4-nodes
  return this.balance(node);
}

function moveRedRight(
  node: RBTNode<Key, Value>,
): RBTNode<Key, Value> {
  this.flipColors(node);

  if (RBTNode.isRed(node.left?.left)) {
    node = this.rotateRight(node);
    this.flipColors(node);
  }

  return node;
}

Note: See the code for balance bellow - in the full implementation.

Delete Max Example 1

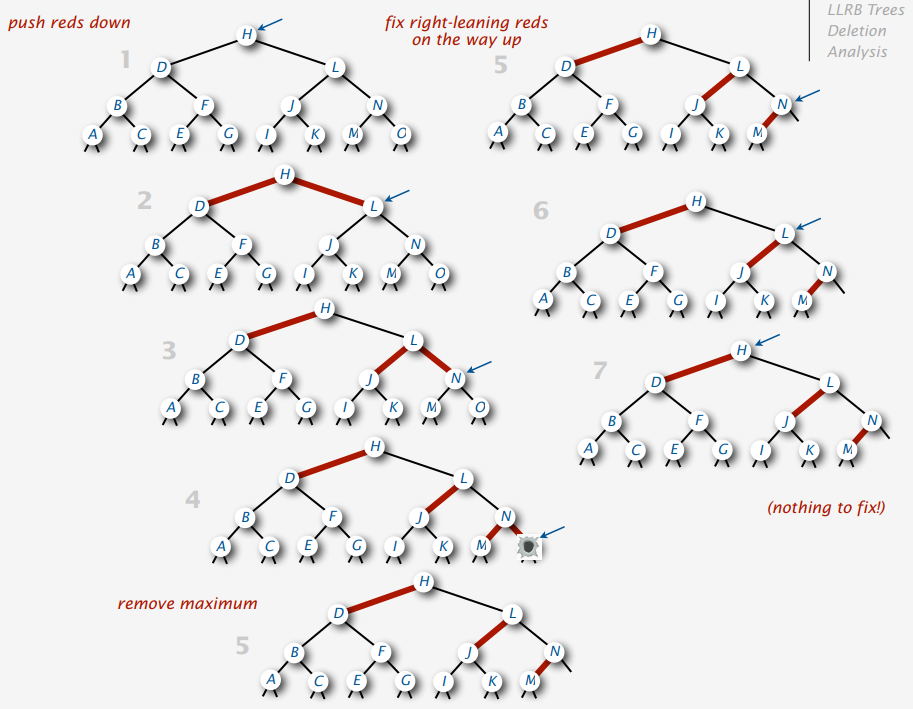
Delete Max Example 2

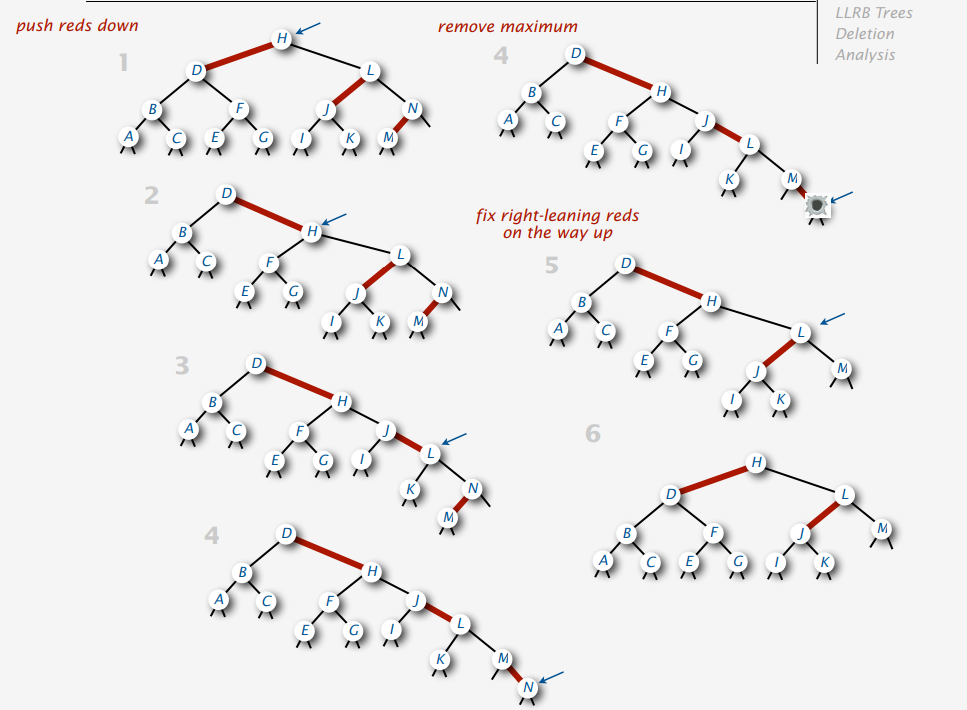
Delete Min

The procedure is the same as when deleting the max only now we traverse the left spine of the tree and on the way down the search path we transform the tree by borrowing from a sibling, the 3-nodes are already leaning left.

function delMin(
  node: RBTNode<Key, Value> | null,
): RBTNode<Key, Value> | null {
  if (node == null) return null;
  if (node.left == null) return null;

  if (
    !RBTNode.isRed(node.left) &&
    !RBTNode.isRed(node.left.left)
  )
    node = this.moveRedLeft(node);

  node.left = this.delMin(node.left);
  return this.balance(node);
}

function moveRedLeft(
  node: RBTNode<Key, Value>,
): RBTNode<Key, Value> {
  this.flipColors(node);

  if (RBTNode.isRed(node.right?.left)) {
    node.right = this.rotateRight(
      node.right as RBTNode<Key, Value>,
    );
    node = this.rotateLeft(node);
    this.flipColors(node);
  }

  return node;
}

Delete Min Example

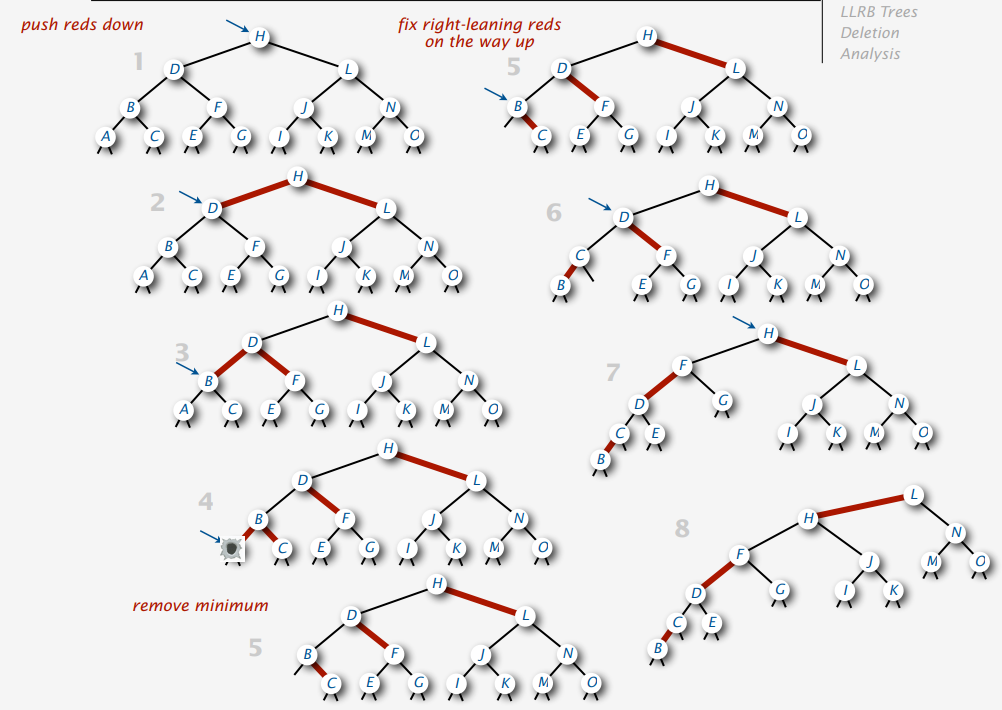
Delete arbitrary node

Deleting an arbitrary node combines the approaches of deleting in a regular BST, deleting min and deleting max in the red-black tree. Search for the node and transform the encountered nodes to either a 3-node or a 4-node, if the node is a leaf just delete it. If the search ends on a non leaf node, find it's successor - min of right subtree, swap their places and delete the min in the right subtree. Fix the nodes on the way up - make the right leaning 3 nodes lean leaf and break up any 4-nodes.

function del(
  node: RBTNode<Key, Value> | null,
  key: Key,
): RBTNode<Key, Value> | null {
  if (node == null) return null;

  if (node.key.compareTo(key) < 0) {
    if (
      !RBTNode.isRed(node.left) &&
      !RBTNode.isRed(node.left?.left)
    )
      node = this.moveRedLeft(node);

    node.left = this.del(node.left, key);
  } else {
    if (RBTNode.isRed(node.left)) node = this.rotateRight(node);

    // Node at bottom, delete it
    if (node.key.compareTo(key) === 0 && node.right === null)
      return null;

    if (
      !RBTNode.isRed(node.right) &&
      !RBTNode.isRed(node.right?.left)
    )
      node = this.moveRedRight(node);

    // Node not at bottom, swap it & delete it from bottom
    if (node.key.compareTo(key) === 0) {
      const nextNode = this.getMinNode(
        node.right as RBTNode<Key, Value>,
      );
      node.key = nextNode.key;
      node.value = nextNode.value;
      node.right = this.delMin(node.right);
    } else {
      node.right = this.del(node.right, key);
    }
  }

  return this.balance(node);
}

Time complexity

The search, insert and delete operations of a red-black tree are O(N) = log(N).

Implementation

Full typescript implementation

/**
Implementable by comparable objects
*/
interface Comparable<T> {
  /**
   * Returns - 1 if this is greater than t,
   * 0 if equal,
   * 1 if this is less than this
   * @param  {T} t
   * @returns number
   */
  compareTo(t: T): number;
}

type RBTNodeColor = 'RED' | 'BLACK';

class RBTNode<Key extends Comparable<Key>, Value> {
  left: RBTNode<Key, Value> | null;
  right: RBTNode<Key, Value> | null;
  key: Key;
  value: Value;
  size: number;
  color: RBTNodeColor;

  constructor(key: Key, value: Value, color: RBTNodeColor) {
    this.key = key;
    this.value = value;
    this.size = 1;
    this.left = null;
    this.right = null;
    this.color = color;
  }

  public static isRed<Key extends Comparable<Key>, Value>(
    node: RBTNode<Key, Value> | null | undefined,
  ): boolean {
    if (node == null) return false;
    return node.color === 'RED';
  }

  public flipColor(): void {
    this.color = this.color === 'RED' ? 'BLACK' : 'RED';
  }
}

class RedBlackTree<Key extends Comparable<Key>, Value> {
  root: RBTNode<Key, Value> | null;

  constructor() {
    this.root = null;
  }

  public get(key: Key): Value | null {
    let x = this.root;

    while (x != null) {
      const cmp = x.key.compareTo(key);
      if (cmp < 0) x = x.left;
      else if (cmp > 0) x = x.right;
      else return x.value;
    }

    return null;
  }

  public put(key: Key, value: Value): void {
    this.root = this.insert(this.root, key, value);
  }

  public deleteMax(): void {
    if (this.root == null) return;

    this.root = this.delMax(this.root);
    if (this.root) this.root.color = 'BLACK';
  }

  public deleteMin(): void {
    if (this.root == null) return;

    this.root = this.delMin(this.root);
    if (this.root) this.root.color = 'BLACK';
  }

  public delete(key: Key): void {
    if (key == null) return;

    this.root = this.del(this.root, key);
    if (this.root) this.root.color = 'BLACK';
  }

  private insert(
    node: RBTNode<Key, Value> | null,
    key: Key,
    value: Value,
  ): RBTNode<Key, Value> {
    if (node == null) return new RBTNode(key, value, 'RED');

    const cmp = node.key.compareTo(key);
    if (cmp < 0) {
      node.left = this.insert(node.left, key, value);
    } else if (cmp > 0) {
      node.right = this.insert(node.right, key, value);
    } else {
      node.value = value;
    }

    return this.balance(node);
  }

  private balance(
    node: RBTNode<Key, Value>,
  ): RBTNode<Key, Value> {
    if (RBTNode.isRed(node.right) && !RBTNode.isRed(node.left))
      node = this.rotateLeft(node);
    if (
      RBTNode.isRed(node.left) &&
      RBTNode.isRed(node.left?.left)
    )
      node = this.rotateRight(node);
    if (RBTNode.isRed(node.left) && RBTNode.isRed(node.right))
      this.flipColors(node);

    node.size =
      1 + this.sizeOf(node.left) + this.sizeOf(node.right);
    return node;
  }

  private rotateLeft(
    node: RBTNode<Key, Value>,
  ): RBTNode<Key, Value> {
    // cast is safe, it cannot be null because it is checked in balance()
    const x: RBTNode<Key, Value> = node.right as RBTNode<
      Key,
      Value
    >;
    const nodeRight: RBTNode<Key, Value> | null = x.left;
    x.left = node;
    x.color = node.color;
    node.right = nodeRight;
    node.color = 'RED';

    return x;
  }

  private rotateRight(
    node: RBTNode<Key, Value>,
  ): RBTNode<Key, Value> {
    // cast is safe, it cannot be null because it is checked in balance()
    const x: RBTNode<Key, Value> = node.left as RBTNode<
      Key,
      Value
    >;
    const nodeLeft: RBTNode<Key, Value> | null = x.right;
    x.right = node;
    x.color = node.color;
    node.left = nodeLeft;
    node.color = 'RED';

    return x;
  }

  private flipColors(node: RBTNode<Key, Value>): void {
    node.flipColor();
    node.left?.flipColor();
    node.right?.flipColor();
  }

  private sizeOf(node: RBTNode<Key, Value> | null): number {
    if (node == null) return 0;

    return node.size;
  }

  private delMax(
    node: RBTNode<Key, Value> | null,
  ): RBTNode<Key, Value> | null {
    if (node == null) return null;

    // Lean 3-nodes to the right
    if (RBTNode.isRed(node.left)) node = this.rotateRight(node);

    if (node.right === null) return null;

    // Borrow from sibling if necessary
    if (
      !RBTNode.isRed(node.right) &&
      !RBTNode.isRed(node.right.left)
    )
      node = this.moveRedRight(node);

    node.right = this.delMax(node.right);

    // Fix right leaning red links and eliminate 4-nodes
    return this.balance(node);
  }

  private moveRedRight(
    node: RBTNode<Key, Value>,
  ): RBTNode<Key, Value> {
    this.flipColors(node);

    if (RBTNode.isRed(node.left?.left)) {
      node = this.rotateRight(node);
      this.flipColors(node);
    }

    return node;
  }

  private delMin(
    node: RBTNode<Key, Value> | null,
  ): RBTNode<Key, Value> | null {
    if (node == null) return null;
    if (node.left == null) return null;

    if (
      !RBTNode.isRed(node.left) &&
      !RBTNode.isRed(node.left.left)
    )
      node = this.moveRedLeft(node);

    node.left = this.delMin(node.left);
    return this.balance(node);
  }

  private moveRedLeft(
    node: RBTNode<Key, Value>,
  ): RBTNode<Key, Value> {
    this.flipColors(node);

    if (RBTNode.isRed(node.right?.left)) {
      node.right = this.rotateRight(
        node.right as RBTNode<Key, Value>,
      );
      node = this.rotateLeft(node);
      this.flipColors(node);
    }

    return node;
  }

  private del(
    node: RBTNode<Key, Value> | null,
    key: Key,
  ): RBTNode<Key, Value> | null {
    if (node == null) return null;

    if (node.key.compareTo(key) < 0) {
      if (
        !RBTNode.isRed(node.left) &&
        !RBTNode.isRed(node.left?.left)
      )
        node = this.moveRedLeft(node);

      node.left = this.del(node.left, key);
    } else {
      if (RBTNode.isRed(node.left))
        node = this.rotateRight(node);

      // Node at bottom, delete it
      if (node.key.compareTo(key) === 0 && node.right === null)
        return null;

      if (
        !RBTNode.isRed(node.right) &&
        !RBTNode.isRed(node.right?.left)
      )
        node = this.moveRedRight(node);

      // Node not at bottom, swap it & delete it from bottom
      if (node.key.compareTo(key) === 0) {
        const nextNode = this.getMinNode(
          node.right as RBTNode<Key, Value>,
        );
        node.key = nextNode.key;
        node.value = nextNode.value;
        node.right = this.delMin(node.right);
      } else {
        node.right = this.del(node.right, key);
      }
    }

    return this.balance(node);
  }

  private getMinNode(
    node: RBTNode<Key, Value>,
  ): RBTNode<Key, Value> {
    if (node.left == null) return node;
    return this.getMinNode(node.left);
  }
}

Some images taken from: https://www.cs.princeton.edu/~rs/talks/LLRB/RedBlack.pdf