MV's blog

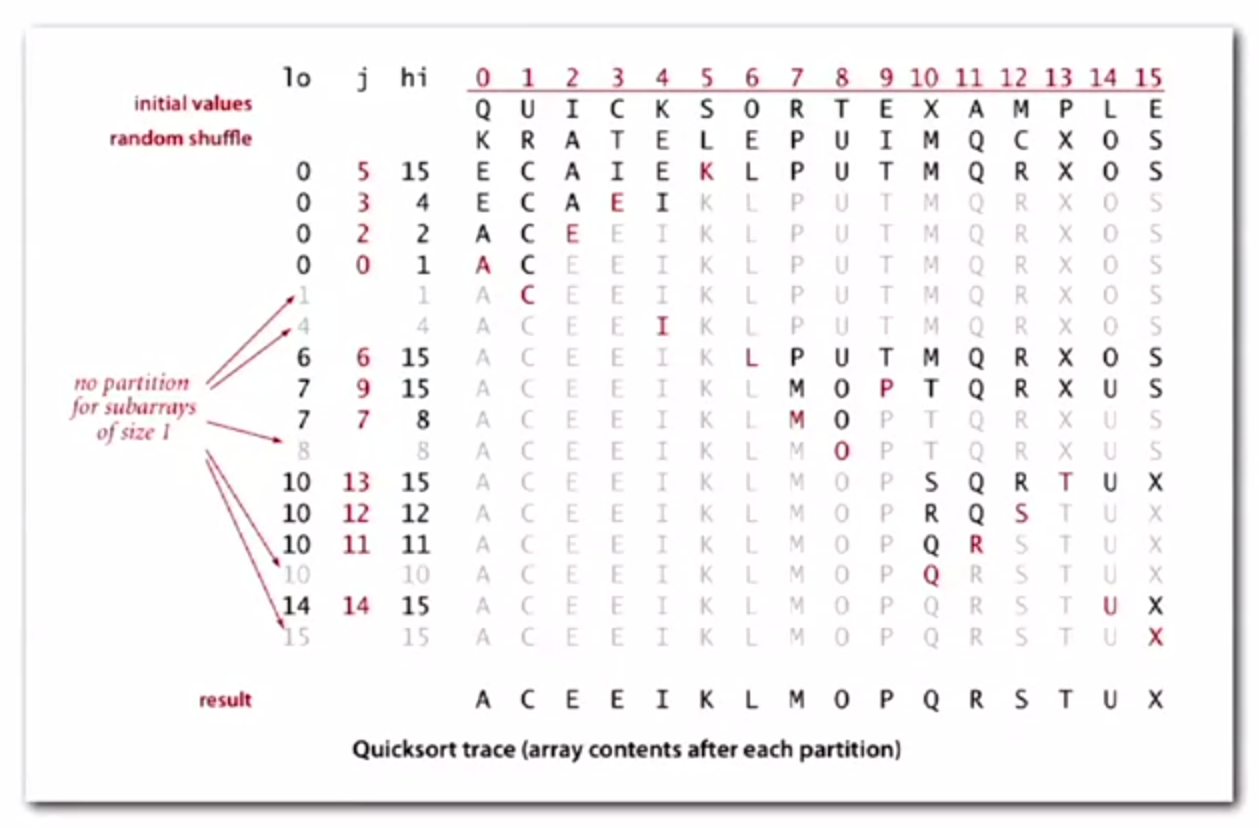
Quick Sort

Quick sort is one of the two classic sorting algorithms that are used widely in the world's computational infrastructure. The idea of quick sort is to partition and sort an array so that for some j, entry n[j] is in place -- no larger entry to the left of j and no smaller entry to the right of j. Repeat recursively for subarrays [0, j) and (j, n.length - 1].

The sorting of the array so that entry n[j] is in place and there are no larger entries to the left and no smaller entries to the rights is as follows:

1. Arbitrarily choose the first element as the pivot/partitioning element
2. Maintain an i pointer that movest left to right
3. Maintain a j pointer that moves right to left
4. Move the i pointer to the left as long as n[i] < n[start]
5. Move the j pointer to the left as long as n[i] > n[start]
6. if the pointers have crossed swap n[j] with n[start]
   • break, sort complete
7. If the pointers have not crossed swap n[i] with n[j]
8. Go to step 4

Time complexity

Worst case: If the pivot element is the max or the min element the performance is O(N) = N2. To make that unlikely to happen we first shuffle the array and the performance becomes O(N) = N * log(N)

Example:

Sample typescript implementation for sorting numbers in ascending order.

function quickSort(numbers: number[]): void {
  debugger;
  shuffle(numbers);
  sort(numbers, 0, numbers.length - 1);
}

function shuffle(numbers: number[]): void {
  for (let i = numbers.length - 1; i > 0; i--) {
    const j = Math.floor(Math.random() * (i + 1));
    const tmp = numbers[i];
    numbers[i] = numbers[j];
    numbers[j] = tmp;
  }
}

function sort(
  numbers: number[],
  start: number,
  end: number,
): void {
  if (start >= end) return;

  const j = partition(numbers, start, end);
  sort(numbers, start, j - 1);
  sort(numbers, j + 1, end);
}

function partition(
  numbers: number[],
  start: number,
  end: number,
): number {
  const lo = numbers[start];
  let i = start + 1;
  let j = end;

  while (true) {
    if (numbers[i] < lo && i < end) {
      i++;
      continue;
    }

    if (numbers[j] > lo && j > start) {
      j--;
      continue;
    }

    if (i >= j) {
      break;
    }

    const tmp = numbers[i];
    numbers[i] = numbers[j];
    numbers[j] = tmp;
  }

  const tmp = numbers[j];
  numbers[j] = lo;
  numbers[start] = tmp;

  return j;
}

Image taken from: https://www.coursera.org/learn/algorithms-part1/