MV's blog

Disjoint Sets

A disjoint-set data structure, also called a union–find data structure or merge–find set, is a data structure that stores a collection of disjoint (non-overlapping) sets. Equivalently, it stores a partition of a set into disjoint subsets. It is used for solving connectivity problems like the one illustrated in the image bellow.

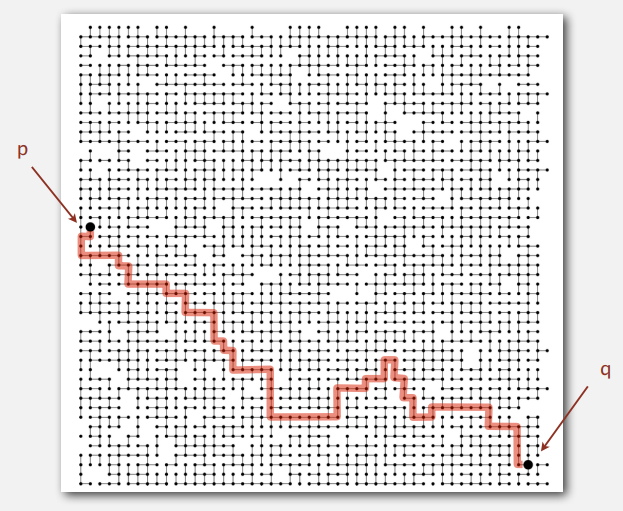
Is there a path connecting the objects p and q ?

Implementation

There are 4 implementations of the disjoint set data structure. quick-find [eager approach], quick union [lazy approach], weighted quick union & weighted quick union with path compression.

Quick-Find [eager approach]

Represent each object as an index in an array, store a same id for objects that are connected. The number of unique ids represents how many connected components or disjoint subsets there are.

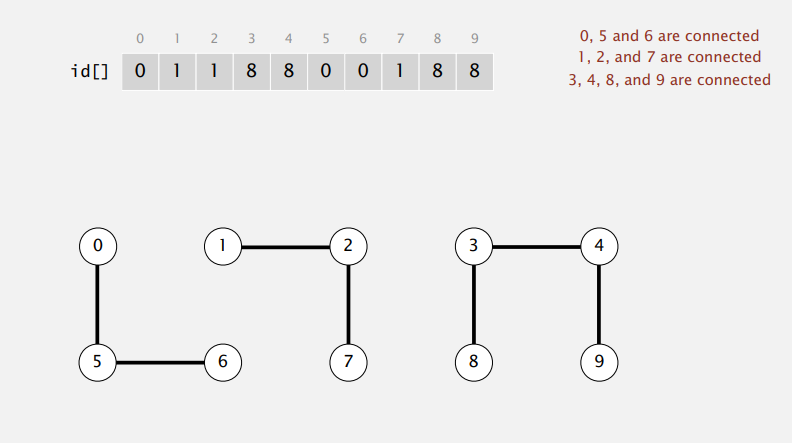
Find operation: Check if p and q have the same id. Cost: O(1)

Union operation: Merge components containing p and q by changing all entries whose id equals id[p] to id[q]. Problem: many values can change.

In this implementation the union operation is too expensive. It takes O(N²) array accesses to process a sequence of N union commands on N objects.

Quick Union [lazy approach]

Represent each object as an index in an array, at each index store the parent of that object.

Find operation: Check if p and q have the same root. The cost of the operation dependends on the depth of the tree. There is a potential that performing the union operations would lead to creating a tree with a single branch in which case the Cost: O(N).

Union operation: Merge components containing p and q by changing the id of p's to the id of q's root. The cost of the union operation itself is O(1) but as noted above, the worst case scenario cost for the find operation is O(N).

In this implementation the find operation in the worst case scenario is too expensive. It takes O(N²) array accesses to process a sequence of N union commands on N objects.

Weighted Quick Union

Represent each object as an index in an array, at each index store the parent of that object.

In a seprate array for each object store the size of it's subtree. Balance the tree by linking the root of the smaller tree to the root of the larger tree.

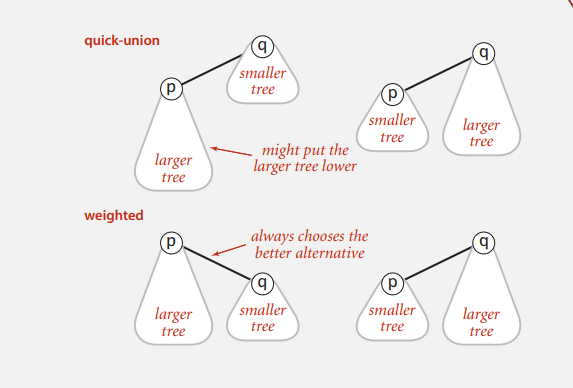
Find operation: Check if p and q have the same root. The cost of the operation dependends on the depth of the tree. Depth of any node x is at most lg(N). When does depth of x increase? It increases by 1 when the tree T1 containing x is merged into another tree T2. ・The size of the tree containing x at least doubles since | T₂ | ≥ | T₁ |.

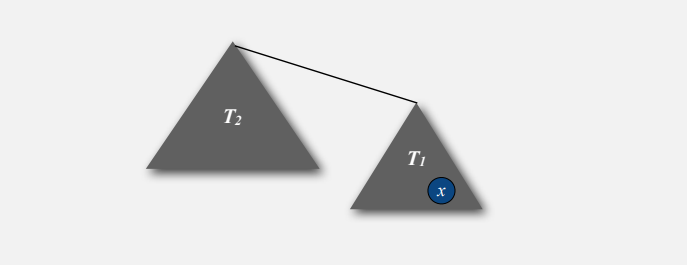
Union operation: Merge components containing p and q by linking the root of the smaller tree to the root of the larger tree. Cost: O(1)

Typescript Implementation:

export class WeightedQuickUnionFind {
  private n: number;
  private objects: Array<number>;
  private size: Array<number>;

  constructor(n: number) {
    if (n <= 0) throw new RangeError();

    this.n = n;
    this.objects = new Array<number>(n);
    this.size = new Array<number>(n);

    for (let i = 0; i < this.n; i++) {
      this.objects[i] = i;
      this.size[i] = 1;
    }
  }

  private root(q: number): number {
    while (this.objects[q] !== q) q = this.objects[q];
    return q;
  }

  public union(p: number, q: number): void {
    const rootP = this.root(p);
    const rootQ = this.root(q);

    if (rootP === rootQ) return;

    if (this.size[rootP] >= this.size[rootQ]) {
      this.objects[rootQ] = rootP;
      this.size[rootP] += this.size[rootQ];
    } else {
      this.objects[rootP] = rootQ;
      this.size[rootQ] += this.size[rootP];
    }
  }

  public connected(p: number, q: number): boolean {
    return this.root(p) === this.root(q);
  }
}

GitHub Repo with sample implementation of a problem/solution: https://github.com/kwml/data-structures-algorithms/tree/master/disjoint-sets

Images taken from: https://www.coursera.org/learn/algorithms-part1/