MV's blog

Binary Search Trees

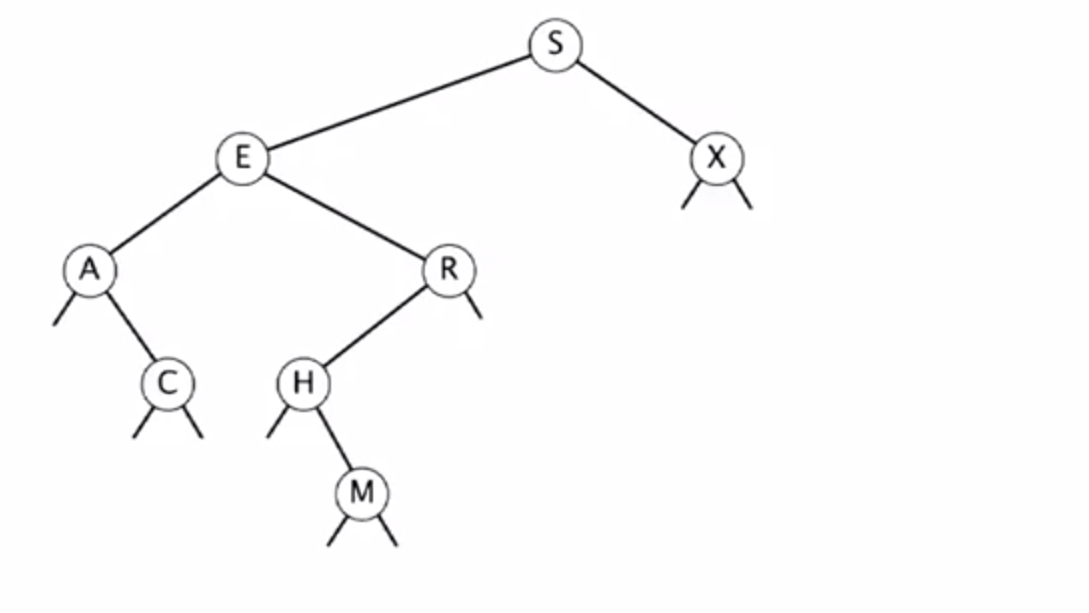
A binary search tree is a binary tree in symetric order. It has nodes which contain information and each node has two links to binary trees that are disjoint from one another -- a left tree and a right tree. The links can also be null, i.e the left tree can be null, the right tree can be null or both can be null. In a binary search tree each node has a key and its key is greater than all the keys in its left subtree and smaller than all the keys in its right subtree.

Operations

A binary search tree can support many operations such as: min(), max(), floor(), ceil() etc.. but the main ones are get(), insert() and delete().

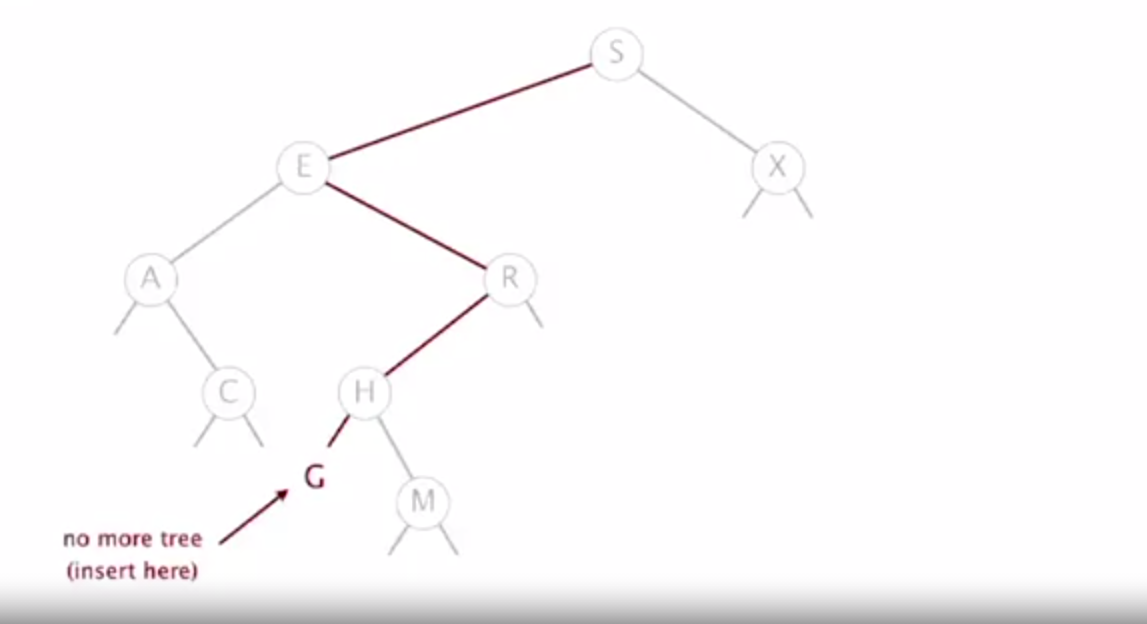
Insert

When inserting a node, start from the root and compare the key's values, if the key to be inserted is less than the root's key, go left, if it is greater go right, repeat until a key with the same value is found in which case replace the old value with the new value, or if no key is found insert the new key at that position.

Search

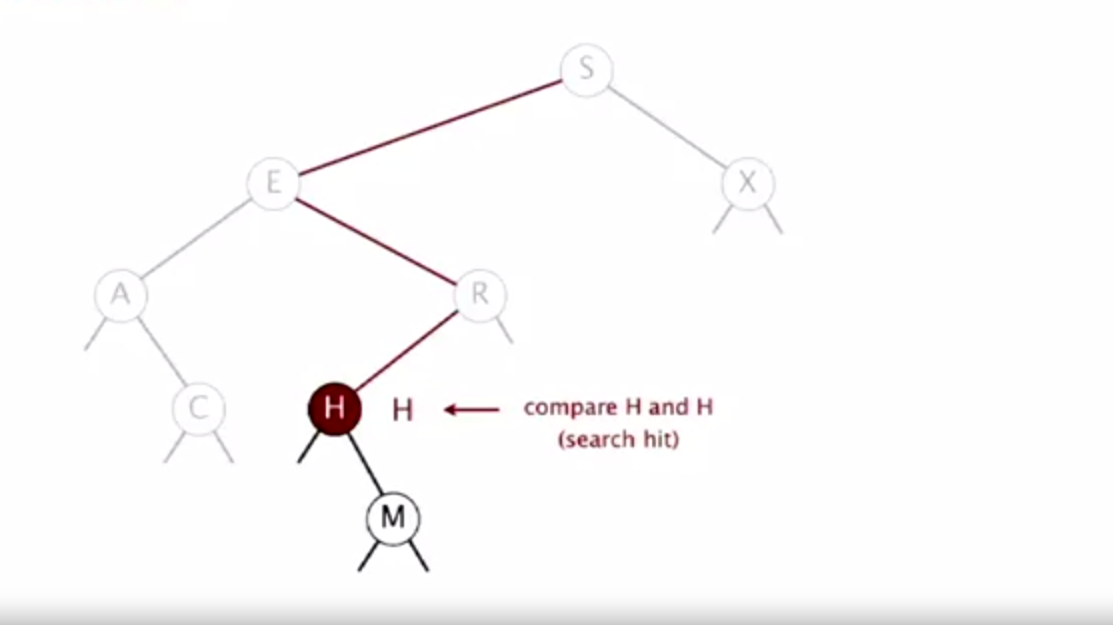
When searching for a node, start from the root and compare the key's values, if the key to be found is less than the root's key, go left, if it is greater go right, repeat until a key with the same value is found in which return the value asssociated with that key, or if no key is found return null;

Delete

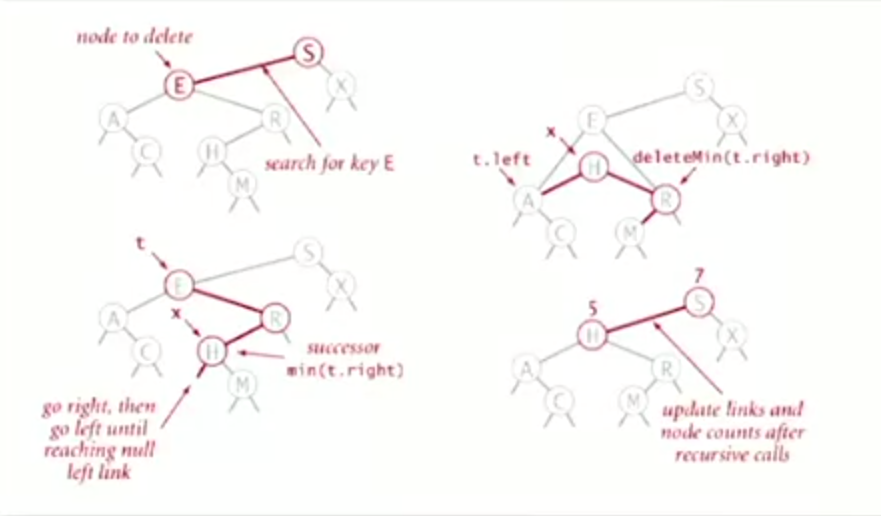
When deleting a node, there are 3 cases to consider.

1. When there is a left subtree and no right subtree in which case the parent left or right link needs to be updated to point to the node's left subtree.
2. When there is a right subtree and no left subtree in which case the parent left or right link needs to be updated to point to the node's right subtree.
3. When there is a left and a right subtree, in which case find the minimum of node's right subtree and put it the place of the node to be deleted, i.e find the next biggest node compared to the node to be deleted and put it in its place. N.B that this operation is not symmetrical.

Time complexity

The time complexity of the BST greatly depends on the order of it's input. In the worst case - inserting keys of ascending or descending order it will be like that of a linked list O(N). If the keys are inputed in a random order the time complexity of the insert and search operation is O(N) = log(N), but the time complexity of the delete operation is sqrt(N), which can in turn make the other operations of the BST sqrt(N) because it is not symmetric.

Implementation

Sample typescript implementation

/**
Implementable by comparable objects
*/
interface Comparable<T> {
  /**
   * Returns - 1 if this is greater than t,
   * 0 if equal,
   * 1 if this is less than this
   * @param  {T} t
   * @returns number
   */
  compareTo(t: T): number;
}

class BSTNode<Key extends Comparable<Key>, Value> {
  left: BSTNode<Key, Value> | null;
  right: BSTNode<Key, Value> | null;
  key: Key;
  value: Value;
  size: number;

  constructor(key: Key, value: Value) {
    this.key = key;
    this.value = value;
    this.size = 1;
    this.left = null;
    this.right = null;
  }
}

class BST<Key extends Comparable<Key>, Value> {
  root: BSTNode<Key, Value> | null;

  constructor() {
    this.root = null;
  }

  public get(key: Key): Value | null {
    let x = this.root;

    while (x != null) {
      const cmp = x.key.compareTo(key);
      if (cmp < 0) x = x.left;
      else if (cmp > 0) x = x.right;
      else return x.value;
    }

    return null;
  }

  public put(key: Key, value: Value): void {
    this.root = this.pvtPut(this.root, key, value);
  }

  public delete(key: Key): void {
    if (key == null) return;

    this.del(this.root, key);
  }

  private pvtPut(
    node: BSTNode<Key, Value> | null,
    key: Key,
    value: Value,
  ): BSTNode<Key, Value> {
    if (node == null) return new BSTNode(key, value);

    const cmp = node.key.compareTo(key);
    if (cmp < 0) {
      node.left = this.pvtPut(node.left, key, value);
    } else if (cmp > 0) {
      node.right = this.pvtPut(node.right, key, value);
    } else {
      node.value = value;
    }

    node.size =
      1 + this.sizeOf(node.left) + this.sizeOf(node.right);
    return node;
  }

  private sizeOf(node: BSTNode<Key, Value> | null): number {
    if (node == null) return 0;

    return node.size;
  }

  private del(
    node: BSTNode<Key, Value> | null,
    key: Key,
  ): BSTNode<Key, Value> | null {
    if (node == null) return null;

    const cmp = node.key.compareTo(key);
    if (cmp < 0) {
      node.left = this.del(node.left, key);
    } else if (cmp > 0) {
      node.right = this.del(node.right, key);
    } else {
      if (node.left == null) return node.right;
      if (node.right == null) return node.left;

      const subMin = this.min(node.right);
      node.key = subMin.key;
      node.value = subMin.value;
      node.right = this.delMin(node.right);
    }

    node.size =
      1 + this.sizeOf(node.left) + this.sizeOf(node.right);
    return node;
  }

  private delMin(
    node: BSTNode<Key, Value>,
  ): BSTNode<Key, Value> | null {
    if (node.left == null) return node.right;

    node.left = this.delMin(node.left);
    node.size =
      1 + this.sizeOf(node.left) + this.sizeOf(node.right);

    return node;
  }

  private min(node: BSTNode<Key, Value>): BSTNode<Key, Value> {
    if (node.left == null) return node;
    return this.min(node.left);
  }
}

Images taken from: https://www.coursera.org/learn/algorithms-part1/