2-3 Trees
A 2-3 tree is a way to generalize a binary search tree and guarantee fast performance. In a 2-3 tree each node can have either one or two keys, if it has two keys it has to have 3 children. In a regular BST node - a 2 node, there is one link for keys that are less than the key in the node, and one link for keys that are greater. In a 3 node, there are 3 links, one link for keys that are less than the keys in the node, one link for keys that are between the keys in the node and one for keys that are greater. A key property of the 2-3 tree is that it is perfectly balanced, i.e every path from the root node to a null link has the same height.
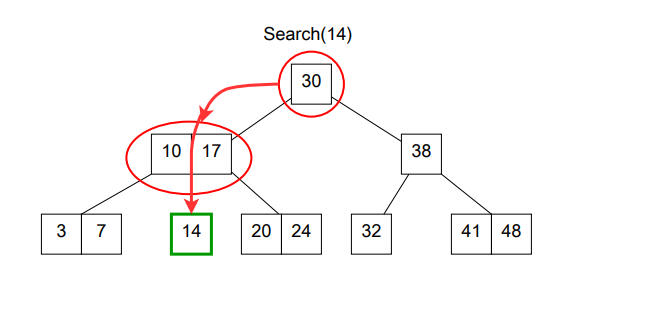
Search
Searching is very similar to searcing in a regular BST, start
from the root and compare the key's values, if the key to
be found is less than the root's key, go left, if it is
greater go right, if the root(node) has 2 keys and the
key is between the node's keys go in the middle. repeat
until a key with the same value is found in which return
the value asssociated with that key, or if no key is found
return null;
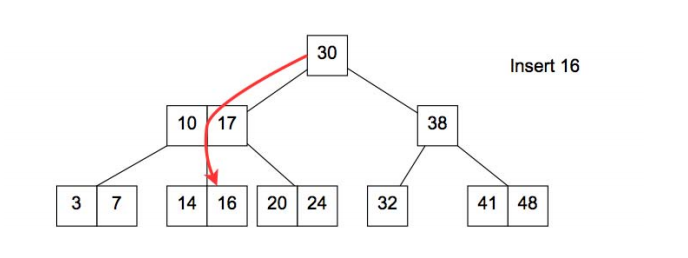
Insert
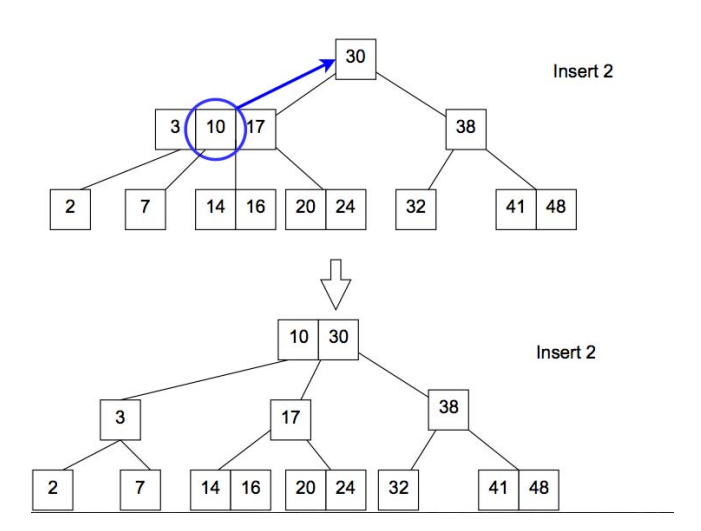
When inserting, the insert can happen in a 2-node or a 3-node.
If the insert is in a 2-node it is the same as in a binary search tree, i.e try to find the node with the same key, if it exists replace the value, if it does not exist create the node.
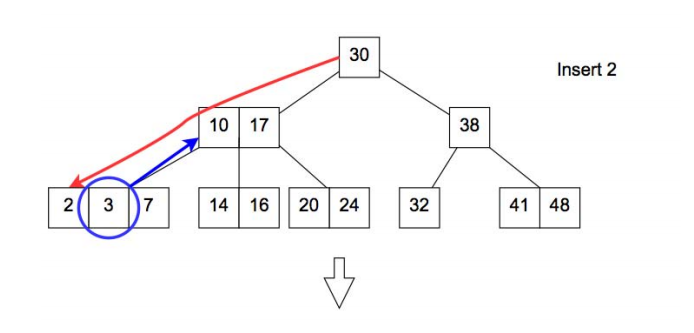
If the insert is in a 3 node, the key is temporarily inserted in the node making it a 4-node, after that the middle key is propagated up to it's parent thus converting the overflowing 4-node to a 3-node again. The process is propagated recursively upwards until there are no more 4-nodes or if it reaches the root and it makes it a 4 node, the root is split and thus increasing the height of the tree by 1.
N.B That BST's height increases by adding nodes at the bottom where as the 2-3 tree's height increases by back propagating a node to the root.
Delete
When deleting, delete a leaf node, if the selected node is not a leaf swap it with its inorder successor thus making it a leaf node and delete it. After that, if what is left is a 2-node, the operation is complete.
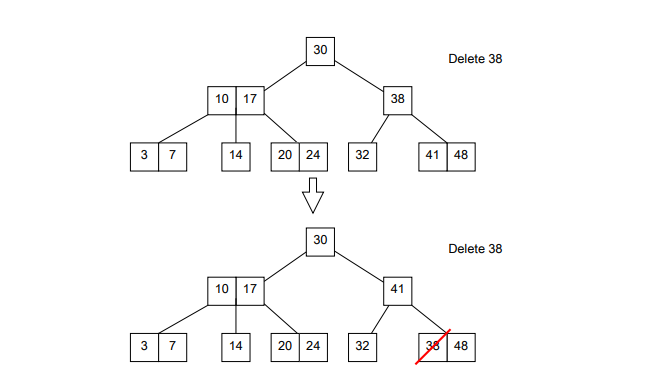
But if what is left is a null(empty) node, that violates the perfectly balanced invariant. When a null(empty) node is left as a result of the delete operation, i.e the node is underflowing, the tree's balance needs to be fixed. That is achieved in 2 ways.
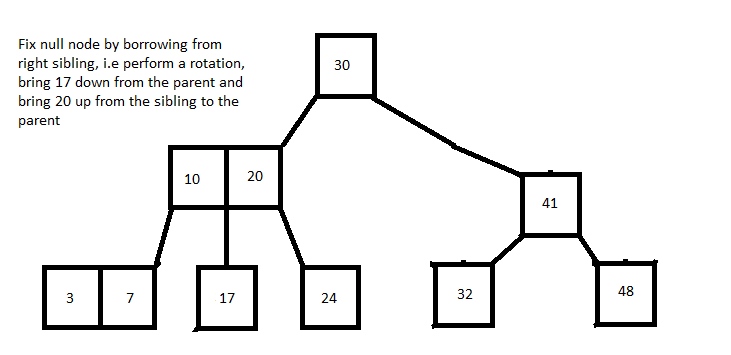
If the node has a 3-node sibling, it can borrow an element from that sibling thus converting itself from a null node to a 2-node and converting it's sibling from a 3-node to a 2-node. The borrowing is actually a rotation in which an element from the parent is brought down and a key from the sibling is brought up to a parent.
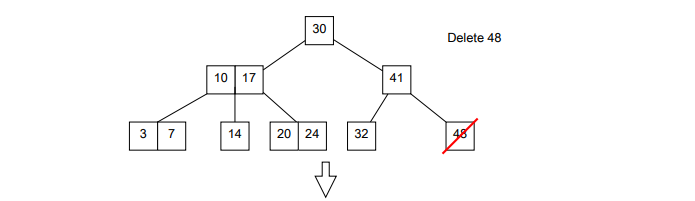
If the node does not have a 3 node sibling, a merge is performed by taking a key from the parent and the sibling thus creating a 3 node. This can leave the parent either a 2 node in which case the operation is done or if the parent was a 2-node it will become a null(empty) node in which case the same rules for fixing the null node apply -- either borrow from a sibling or merge sibling with a key from parent.
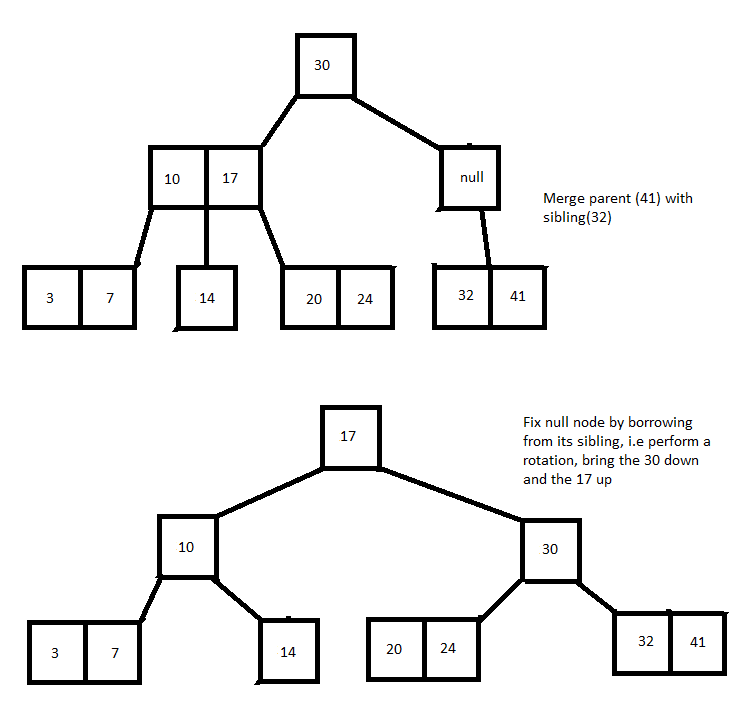
Paint FTW!
Time complexity
The search, insert and delete operations of a 2-3 tree are log3(N) <= O(N) <= log2(N).
Implementation
The implementation of 2-3 trees is not straightforward because it requires a lot of deliberation of the different types of nodes and their possible configurations. However, knowledge of how they work is very beneficial for Red-Black trees which are much more easily implementable. They are also very beneficial for their more general form - the B-Trees.
Some images taken from: https://ocw.mit.edu/courses/electrical-engineering-and-computer-science/6-046j-design-and-analysis-of-algorithms-spring-2015/recitation-notes/MIT6_046JS15_Recitation2.pdf/


